Алексей Семенов, д. т. н., профессор кафедры технологий информационного и математического моделирования СПбГАСУ, разрабатывает математические модели, алгоритмы и программное обеспечение для исследования колебаний и напряжённо-деформированного состояния оболочечных конструкций при разных видах динамического нагружения. В том числе – и при действии взрывной нагрузки. Работа поддержана грантом на выполнение научно-исследовательских работ научно-педагогическими работниками Санкт-Петербургского государственного архитектурно-строительного университета в 2025 г.
В связи с тем, что процесс деформирования тонкостенных оболочек существенно нелинеен, их моделирование и исследование представляет собой сложную задачу, требующую значительных вычислительных ресурсов и разработки специализированного программного обеспечения. Кроме того, на адекватность получаемых при расчётах результатов влияет учёт различных факторов, таких как поперечные сдвиги, ортотропия материала, геометрическая нелинейность. При динамических воздействиях одним из ключевых факторов является учёт демпфирования.
Предлагаемая математическая модель строится на основе гипотез модели Тимошенко (Миндлина – Рейсснера, FSDT) и позволяет учитывать инерцию вращения и поперечные сдвиги. Уравнения Эйлера – Лагранжа дополняются слагаемым, учитывающим демпфирование на основе функции диссипации Рэлея. В известных работах функция диссипации Рэлея записана для модели деформирования конструкции без учёта поперечных сдвигов (модель Кирхгофа – Лява, Койтера, CSDT). Получаемая таким образом система дифференциальных уравнений далее решается одним из численных методов, например, методом Розенброка.
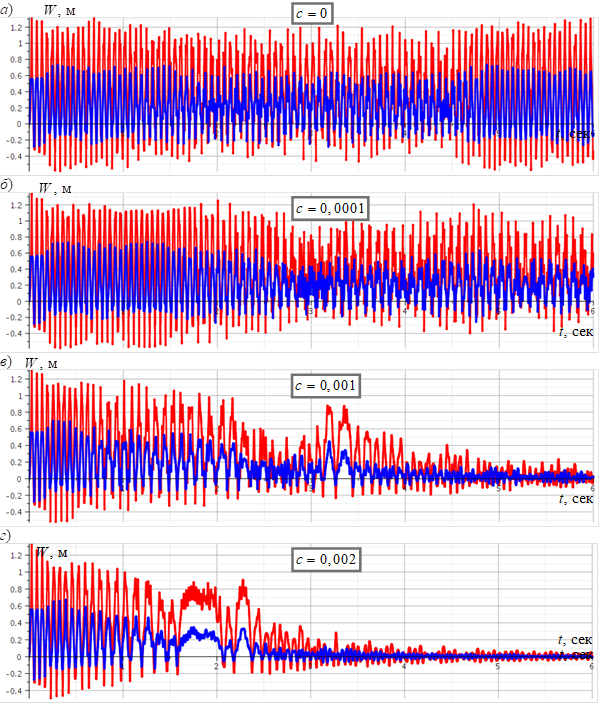
На рис. 1 показан пример получаемых расчётных данных для тонкостенной оболочки при выборе разных значений коэффициента в функции диссипации Рэлея.
Предложенная математическая модель с использованием функции диссипации Рэлея позволяет расширить применимость разработанных ранее автором моделей и алгоритмов расчёта на более широкий класс задач, в том числе моделировать динамический отклик конструкции на действие взрывной нагрузки, когда время приложения нагрузки мало, а колебательный процесс предполагает затухание.