Aleksey Semenov, DSc in Engineering and Professor at the SPbGASU Department of Information and Mathematical Modeling Technologies, is developing mathematical models, algorithms, and software for studying the vibrations and stress-strain state of shell structures under various types of dynamic loading, including explosive loading. This work was supported by a grant for research by academic staff from the St Petersburg State University of Architecture and Civil Engineering in 2025.
Because the deformation process of thin-walled shells is highly nonlinear, their modeling and analysis is a complex task requiring significant computational resources and specialized software development. Furthermore, the validity of the calculation results is affected by consideration of various factors, such as transverse shear, material orthotropy, and geometric nonlinearity. For dynamic loads, damping is a key factor.
The proposed mathematical model is built based on the hypotheses of the Timoshenko (Mindlin-Reissner, FSDT) model and accounts for rotational inertia and transverse shear. The Euler-Lagrange equations are supplemented by a term accounting for damping based on the Rayleigh dissipation function. In well-known studies, the Rayleigh dissipation function is written for a model of structural deformation without accounting for transverse shear (the Kirchhoff-Love, Koiter, and CSDT models). The resulting system of differential equations is then solved using a numerical method, such as Rosenbrock's method.
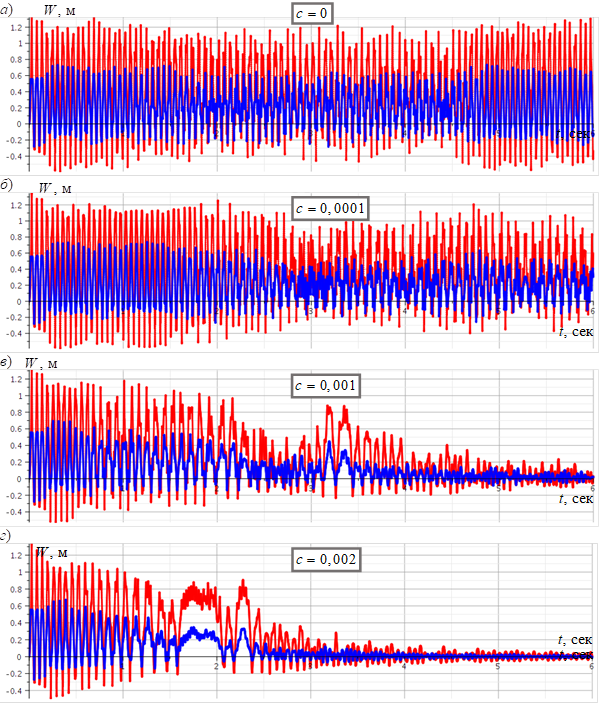
Fig. 1 shows an example of the obtained calculation data for a thin-walled shell when choosing different values of the coefficient in the Rayleigh dissipation function.
The proposed mathematical model using the Rayleigh dissipation function allows us to expand the applicability of the models and calculation algorithms previously developed by the author to a wider class of problems, including modeling the dynamic response of a structure to an explosive load when the load application time is short and the oscillatory process involves damping.